二分法查找——利用指数爆炸进行查找

1. 指数爆炸是什么？有何威力？

假设现在有一第厚度1mm的纸，可以对折无数次。每对折1次，厚度便翻一番。已知地球距离月亮约有39万公里，请问对折多少次后厚度能超过地月距离呢？想想看，39万公里和1mm，差距何等苣大？肯定得对折个几百上千万次吧？好吧，我们来看看：

1mm对折1次变成2mm，再对折一次变成4mm…… 大家可以写几行代码试下看，需要循环几次能超过39万。

procedure TForm1.FormCreate(Sender: TObject);
var
  i, j: Int64;
begin
  j := 1;
  i := 0;
  while j < 390000000000 do begin
    j := j * 2;
    Inc(i);
  end;
  ShowMessage(IntToStr(i));
end;

运行看看。结果是39次！怎么可能只有39次？程序出错了？呵呵，你想多了，程序没错的。仅仅对折了39次，就让1mm的纸厚度超过了地月距离，太让人吃惊了！这就是指数爆炸的威力，远远超乎人们的想像。

2. 二分法查找

我们从上面的例子已经能体会到指数爆炸的历害，现在来思考如何借助指数爆炸的力量！

先来思考下这个问题：有15个犯人排成一排，其中只有1个是杀人犯。你要通过问他们“谁是杀人犯？”来找出这个杀人犯。假设选择其中1人问话会得到以下3种答案：

(1) “我是杀人犯” （询问对象找到时）
(2) “杀人犯在我左这”
(3) “杀人犯在我右边”

这时，应该才能以最少的问话次数，在这15人中找到那个杀人犯呢？

15人有点多，我们先缩小下规模，假设杀人犯在3人中。这种情况下，只要向中间的那个人提问，就能确定谁是杀人犯。中间的人不一定必须就是杀人犯。但即使这样，我也也可以根据中间的人的回答确定谁是杀人犯。

按照这个思路，当人数为15人时，又该怎么提问呢？

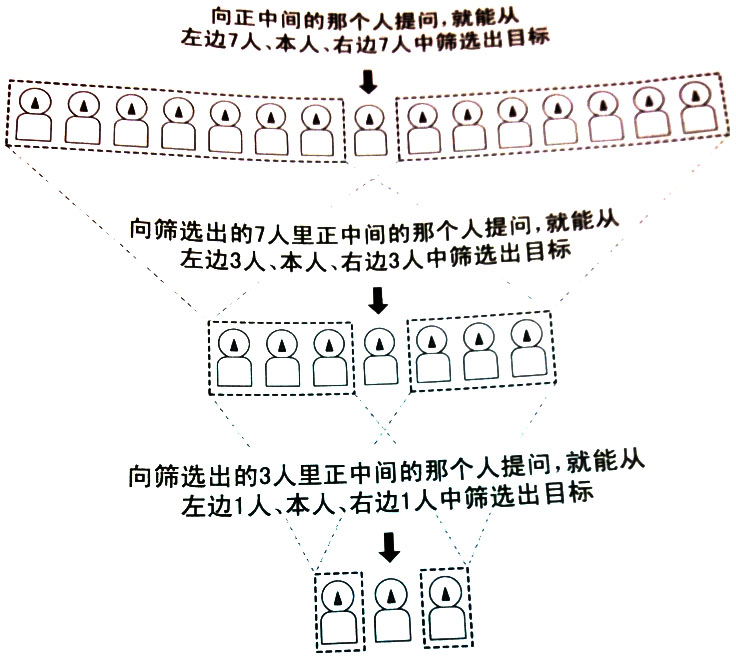
【第一次提问】首先，向15里正中间的那个人提问

这时，我们知道杀人犯在左边7人、中间、右边7人这三组的其中一组中。如果中间的被问话人就是杀人犯，那么提问结束。

【第二次提问】接着，向筛选出的7人里正中间的那个人提问

这时，我们知道杀人犯在左边3人，中间、右边3人这三组的其中一组中。如果中间的被问话人就是杀人犯，那么提问结束。

【第三次提问】最后，向筛选出的3人里正中间的那个人提问

这时，我们知道杀人犯在左边1人、本人、右边1人这三组的其中一组中。这样就可以找出杀人犯了。

如下图所示：

假设右起第5人是杀人犯，问话的范围依次缩小为15人–>7人–>3人–>1人。关键之处在于向正中间的人提问1次，就能筛选掉近1半的人。实际上，这里隐藏着使用第 n-1 层问题来表示第 n 层问题的递归结构。这里所说的“第n层”中的n，就是“剩余提问次数”。即通过n次提问，可以在人中确定杀人犯。

上述“寻找杀人犯”的例子中使用的方法，就是我们在计算机中查找数据时常用的“二分法查找”。

二分法查找（binary search ) 是在有序数据中找出目标数据时 “总是判断目标数据所在范围内正中间的数据” 的方法。也叫做“二分法”、“二分查找”。

在“寻找杀人犯”的例子只是在15个目标中查找，15个目标并不算多，从边上开始判断也花不了太多工夫。不过，要知道二分法查找使用了“指数爆炸”的方法。二分法查找在大量数据中进行查找时，会发挥出巨大的威力。倒如，仅判断10次，就能在2047个数据中找到目标数据。判断20次就能在209万7151个数据中找到目标数据。判断30次就能在21亿4748万3647个数据中找到目标数据。

二分法查找的关键在于，每判断1次就能筛选出近一半的查找对象。因此，必须将查找对象“有序”排列。否则，判断时就不能确定目标数据“在左边还是在右边”了。所以，在“找杀人犯”的问题中，排成一排的人都知道杀人犯在自己的左边还是右边。

用二分法查找，每判断1次就能筛选出近半数查找对象。换言之，多判断1次就能从近2倍的查找对象中找出目标数据。二分法查找正是有效的利用了指数爆炸，才能有此威力，大家明白吧？

下面给出来自网络实现的二分查找算法供大家参考：

非递归实现:

    #include <iostream>  
    using namespace std;  
      
    int binarySearch(int * a, int x, int y, int v)//半开区间[x,y)  
    {  
        int m;  
        while(x < y)  
        {  
            m = x + (y-x)/2;  
            if(v == a[m]) return  m;//找到了  
            else if(v < a[m]) y = m;//在左边  
            else x = m+1;//在右边  
        }  
        return -1;  
    }  
      
    int main()  
    {  
        int n;  
        int a[100];  
        cin >> n;  
        for(int i = 1; i <= n; i ++) scanf("%d",&a[i]);  //输入数据  
      
        cout << binarySearch(a,1,n+1,3) <<endl;  
      
        return 0;  
    }

递归实现:

    #include <iostream>  
    using namespace std;  
      
    int binarySearch(int * a, int x, int y, int v)//半开区间[x,y)  
    {  
        if(y-x == 1){//递归边界处理  
            if(v == a[x]) return x;  
            else return -1;//所找元素不存在  
        }  
        else//尚未达到边界，继续划分  
        {  
            int m = x + (y-x)/2;  
            if(v == a[m]) return m;  
            else if(v < a[m]) //在左边查找  
                return binarySearch(a,x,m,v);  
            else //在右边查找  
                return binarySearch(a,m+1,y,v);  
        }  
    }  
      
    int main()  
    {  
        int n;  
        int a[100];  
        cin >> n;  
        for(int i = 1; i <= n; i ++) scanf("%d",&a[i]);  //输入数据  
      
        cout << binarySearch(a,1,n+1,3) <<endl;  
      
        return 0;  
    }

参考资料：

《程序员的数学》

http://blog.csdn.net/hewu51400206/article/details/6957677

登录