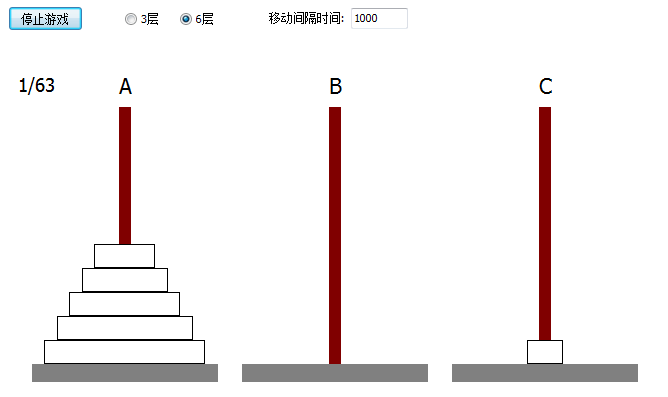
“汉诺塔”是一个由数学家爱德华·卢卡斯于1883年发明的一个非常著名的游戏。游戏的内容是,有三根细柱(A,B,C),A柱上套着6个圆盘。这些圆盘大小各异,按从大到小的顺序自下而上摆放。如下图所示。
(图上白色黑框的代表圆盘)
现在要把套在A住上的6个圆盘全部移到B柱上。并且在移动圆盘时须遵守下述规则:
- 一次只能移动柱子最上端的一个圆盘。
- 小圆盘上不能放大圆盘。
将1个圆盘从一根柱子移到另一根柱子,算移动“1次”。那么,将6个圆盘全部从A移到B需要移动几次呢?(大家可以先默想一下)
让我们来看看C语言编写的解法程序吧,这是一个递归的调用:
void hanoi(int n, char x, char y, char z) {
if (n == 0) {
/* 什么也不做 */
} else {
hanoi(n-1, x, z, y);
printf("%c->%c, ", x, y);
hanoi(n-1, z, y, x);
}
}
int main(void) {
hanoi(6, 'A', 'B', 'C');
return EXIT_SUCCESS;
}
上面的程序会正确的输出“6层汉诺塔”的解决步骤。hanoi 就是核心了,不过上面的C代码并不能直观的显示移动的过程,所以我特别用delphi写了一个小程序,用来做演示。
type
// 用于存放指定轴上第n次移动时圆盘的数量与编号
THanoiValue = record
Start: Integer;
procedure Push(V: Byte);
function Pop(): Byte;
function Count: Integer;
function Get(Index: Integer): Byte;
end;
// 记录每次移动后的状态,以便动画显示
THanoiList = array of THanoiValue;
// 汉诺塔模拟移动
THanoi = class(TObject)
const
SPACE = 24;
private
FCS: TCanvas;
FTimer: TTimer;
FIndex: Integer;
FLayerCount: Integer;
FAxis: array of THanoiList;
FLayerWidth: array of Integer;
FW, FH: Integer;
FXx, FYx, FZx, FIW: Integer;
function GetInterval: Cardinal;
procedure SetInterval(const Value: Cardinal);
protected
procedure Init();
procedure Hanoi(n: Integer; X, Y, Z: Integer);
procedure DoTimer(Sender: TObject);
procedure DoDrawBackground();
procedure DoDrawItem(AIndex: Integer);
procedure DoDraw();
public
constructor Create(CS: TCanvas);
destructor Destroy; override;
procedure Start; // 开始演示
procedure Stop; // 停止演示
// 演示速度
property Interval: Cardinal read GetInterval write SetInterval;
// 几层圆盘? 本示例最多支持7层,受限于THanoiValue的定义,需要更多的话请你改进它
property LayerCount: Integer read FLayerCount write FLayerCount;
end;
{ THanoi }
constructor THanoi.Create(CS: TCanvas);
begin
FCS := CS;
FTimer := TTimer.Create(frmMathTool);
FTimer.Enabled := False;
FTimer.Interval := 1000;
FTimer.OnTimer := DoTimer;
end;
destructor THanoi.Destroy;
begin
Stop();
FreeAndNil(FTimer);
inherited;
end;
procedure THanoi.DoDraw;
begin
DoDrawBackground();
DoDrawItem(0);
DoDrawItem(1);
DoDrawItem(2);
FCS.Font.Size := 14;
FCS.Brush.Color := clWhite;
FCS.TextOut(10, 6, Format('%d/%d', [FIndex, High(FAxis[0])]));
end;
procedure THanoi.DoDrawBackground;
var
R: TRect;
procedure DrawAxis(AOffset: Integer; const AName: string);
begin
FCS.Brush.Color := clMaroon;
R.Left := AOffset + (FIW - 12) shr 1;
R.Right := R.Left + 12;
R.Top := 40;
R.Bottom := FH - SPACE;
FCS.FillRect(R);
FCS.Brush.Color := clWhite;
FCS.TextOut(R.Left, 6, AName);
end;
begin
FCS.Brush.Color := clWhite;
FCS.FillRect(FCS.ClipRect);
FCS.Brush.Color := clDkGray;
SetRect(R, FXx, FH - SPACE, FXx + FIW, FH - 6);
FCS.FillRect(R);
SetRect(R, FYx, FH - SPACE, FYx + FIW, FH - 6);
FCS.FillRect(R);
SetRect(R, FZx, FH - SPACE, FZx + FIW, FH - 6);
FCS.FillRect(R);
FCS.Font.Size := 16;
DrawAxis(FXx, 'A');
DrawAxis(FYx, 'B');
DrawAxis(Fzx, 'C');
end;
procedure THanoi.DoDrawItem(AIndex: Integer);
const
LH = 24;
var
X, Y, I, W: Integer;
V: THanoiValue;
R: TRect;
begin
V := FAxis[AIndex][FIndex];
if V.Count = 0 then Exit;
case AIndex of
0: X := FXx;
1: X := FYx;
2: X := FZx;
else
Exit;
end;
Y := FH - SPACE;
FCS.Brush.Color := clWhite;
for I := 0 to V.Count - 1 do begin
W := FlayerWidth[V.Get(i) - 1];
R.Left := X + (FIW - W) div 2;
R.Right := R.Left + W;
R.Top := Y - LH;
R.Bottom := Y;
Dec(Y, LH);
FCS.Rectangle(R);
end;
end;
procedure THanoi.DoTimer(Sender: TObject);
begin
if FIndex > High(FAxis[0]) then
FTimer.Enabled := False
else begin
DoDraw();
Inc(FIndex);
end;
end;
function THanoi.GetInterval: Cardinal;
begin
Result := FTimer.Interval;
end;
procedure THanoi.Hanoi(n, X, Y, Z: Integer);
begin
if n > 0 then begin
Hanoi(n - 1, x, z, y);
FAxis[y][FIndex].Start := FAxis[y][FIndex - 1].Start;
FAxis[x][FIndex].Start := FAxis[x][FIndex - 1].Start;
FAxis[z][FIndex].Start := FAxis[z][FIndex - 1].Start;
FAxis[y][FIndex].Push(FAxis[x][FIndex].Pop);
Inc(FIndex);
Hanoi(n - 1, z, y, x);
end;
end;
procedure THanoi.Init;
var
I, J: Integer;
begin
I := (2 shl (FLayerCount - 1));
if Length(FAxis) < 3 then begin
SetLength(FAxis, 3);
SetLength(FAxis[0], I);
SetLength(FAxis[1], I);
SetLength(FAxis[2], I);
FillChar(FAxis[0][0], i * 4, 0);
FillChar(FAxis[1][0], i * 4, 0);
FillChar(FAxis[2][0], i * 4, 0);
for i := 1 to FLayerCount do
FAxis[0][0].Push(I);
FIndex := 1;
Hanoi(FLayerCount, 0, 1, 2);
end;
FIndex := 0;
FW := FCS.ClipRect.Right - FCS.ClipRect.Left;
FH := FCS.ClipRect.Bottom - FCS.ClipRect.Top;
FIW := Round((FW - SPACE * 4) / 3);
SetLength(FLayerWidth, FLayerCount);
J := Round(FIW * 0.8 / FLayerCount);
for I := 0 to FLayerCount - 1 do
FLayerWidth[i] := FIW - (I + 1) * J;
FXx := SPACE;
FYx := FXx + FIW + SPACE;
FZx := FYx + FIW + SPACE;
DoDrawBackground();
end;
procedure THanoi.SetInterval(const Value: Cardinal);
begin
FTimer.Interval := Value;
end;
procedure THanoi.Start;
begin
Init;
FTimer.Enabled := True;
end;
procedure THanoi.Stop;
begin
FTimer.Enabled := False;
Init;
end;
{ THanoiValue }
function THanoiValue.Count: Integer;
var
I: Integer;
begin
Result := 0;
I := Start;
while (Result < 10) and (I and $7 > 0) do begin
Inc(Result);
I := I shr 3;
end;
end;
function THanoiValue.Get(Index: Integer): Byte;
var
I, K: Integer;
begin
Result := 0;
I := Start;
K := 0;
while K < 8 do begin
Result := I and $7;
if Result > 0 then begin
if K = Index then
Break;
I := I shr 3;
Inc(K);
end else
Break;
end;
end;
function THanoiValue.Pop: Byte;
var
I, J, K: Integer;
begin
Result := 0;
I := Start;
K := 0;
while K < 8 do begin
J := I and $7;
if J > 0 then begin
Result := J;
I := I shr 3;
Inc(K);
end else begin
if Result > 0 then
Start := Start and (not ($7 shl ((K - 1) * 3)));
Break;
end;
end;
end;
procedure THanoiValue.Push(V: Byte);
var
I, K, L: Integer;
begin
I := Start;
L := V;
K := 0;
while K < 8 do begin
if (I and $7) > 0 then begin
I := I shr 3;
L := L shl 3;
Inc(K);
end else begin
Start := Start or L;
Break;
end;
end;
end;
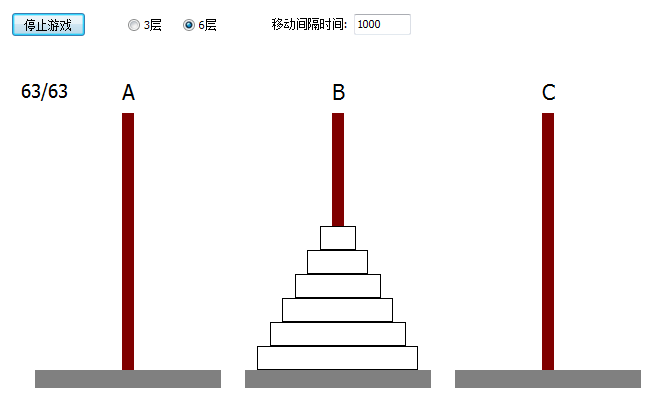
使用 THanoi 可以动态的演示移动过程,我的程序运行效果如下:
在上面的演示程序中,是先将整个移动过程计算好后保存起来,然后用定时器动画显示的。THanoiValue 的作用很关键,它记录了每次移动后在一个轴上的圆盘数量和大小(编号),这样才可以准确的画图展示移动过程。